ミニドローンによる三次元広告の可能性を検証してみた
皆さんこんにちは。
今日はミニドローンを買ったので三次元広告が可能かを検証してみた。
イメージとしてはこんな感じです。

必要なものは
- ミニドローン
amazonとかで8000円程度の小型ドローンがいっぱい売ってますのでなんでもよろしいかと思います。私は世界最小の2.2センチpico droneを出してるTRNDlabsのカメラ付きミニドローンでした。(船便で一ヶ月かかります)
https://www.trndlabs.com/product/skeye-mini-drone-with-hd-camera/
- チラシ
・・・これだけです。
ドローンにチラシをつけることで3次元空間が自由に広告として扱えるようになる、と思いました。
このチラシドローンで広がった夢は
・ビルの一階から上空へ向かってランチ広告を出す。
・要所要所にホバリングさせ、指定の会場への誘導。
・チラシを見ている人たちのモニタリング(いづれは音声案内も)
・チラシの代わりに無人野菜のようにミント等の葉っぱや花を販売
・アダルトなど人が余り介在しない方が良いチラシの配布
など考えました。
しかし、、、
操縦難し過ぎです
慣れとかそういうレベルじゃなくとてもじゃないけど10秒も飛ばしてられないです
カメラとかくるくる回ってそもそもどっち前向いてるかわかりません
結論として今の段階のミニドローンはおもちゃラジコンにカメラが付いたレベルで実用には程遠いです
もちろん最近の航空取材などで使われるドローンは、ホバリングや、スマホからルート指示など出来ますので、そちらはきちんと商業に乗るかと思われます。
さらに都内など人口過密地域は年末あたりからドローン規制法の対象となるっぽいです。
2015年9月4日成立。年内に施行。 飛行に許可が必要な場所の範囲などルールの詳細は今後、国土交通省が省令や通達で定める。人口密度が1平方キロメートルあたり4000人以上の人口集中地区が対象になる方向で、東京都では23区などを含む。飛行時は人や建物と数十メートル離れることを義務付け、違反した場合は50万円以下の罰金。規制を知らずにドローンを飛ばさないよう周知の徹底も課題になる。
どうしてもミニドローンを購入考えてる方は、カメラなんか要らないのでピコドローンでおもちゃとして遊んだ方が良さそうです。

https://www.trndlabs.com/product/skeye-pico-drone/
今回は人柱としてご参考になればと思います
それではまた
ECを支える人工知能の分類と学び方一覧
皆さんこんにちは。
1936年、かつてアランチューリングが書いた論文をもとに「エニグマの暗号を解読するのは人の手では無理だ、難しいことは機械にやってもらおうじゃないか!」という動きができました。
2015年現在、「情報が氾濫しすぎている。人の手では無理だ、多くの情報からコンピュータが勝手に考えて答えを出してよ!」という人工知能に発展してきています。
一言で人工知能といっても流行りのディープラーニングからただの統計のようなものまでたくさん種類があります。
それぞれの特徴を活かし、自然言語処理、画像処理、音声認識、機械学習、ロボティクスなどに応用されていますが、どのような人工知能の種類があるか、現時点で最もAI活用が進んでいる先端のECサイトを例にとって見ていきたいと思います。
| 機械学習の種類 | 特徴 | 手法例 | 使用例 |
|---|---|---|---|
| 教師あり学習 | 事前のサンプルデータをもとにデータの法則性を探す | 回帰分析、SVM | 商品の売れ行き予測、自動発注 |
| 教師なし学習 | サンプルのない中、実データそのものを解析してデータの構造や特徴を抽出する | k-平均法,潜在意味インデックス,トピックモデル手法 | レコメンド機能、評判の解析 |
| 半教師あり学習 | 少数のサンプルを用いて学習を行い、その後ある程度実データを分類して確度が高いものをサンプルとして捉え直して再度学習させる | ブートストラップ法、Adaboost | 商品情報からカタログデータの構築、商品画像の解析 |
| 構造学習 | 個別にデータを推定せずデータ全体の構造に最適化した形で個々の推定をまとめて行う | 構造化SVM、CRF | 商品情報からのカタログデータ構築 |
| 強化学習 | サンプルが存在しない中、学習した後からのフィードバック情報でさらなる学習の手がかりとする | バンディットアルゴリズム、UCBアルゴリズム | レコメンド、サーチ検索の結果、広告のパースナライズ |
| ディープラーニング(深層学習) | 人の脳の構造を模倣しニューラルネットワークという手法を多層化。データを様々な抽象度で学習する | 制限付きボルツマンマシン、Category2Vec | レコメンドの高度化、商品情報の解析、欠損情報の推定 |
- 教師あり学習
教師あり学習とは事前に与えられたサンプルとなるデータを「教師からの例題」とみなしてそれをもとにデータの識別を行う手法です。売れ行き予測や少ない商品群のカテゴライズなどで一般的に使われます。
1.回帰分析
回帰分析は商品の売れ行き予測に使われます。未来の日時における販売量を求めるため、日時、月末、連休、販促活動、温度などの情報を説明変数として、過去の各データを学習させることで関連性、法則性を見出します。これによってマイナー商品も高精度で予測でき、バイヤーなどによる誤発注もなくなるという優れものです。
回帰分析に関してはこちらなどをご参照ください。
2.サポートベクターマシン(SVM)
他にも教師あり学習の手法があります。データを分類する手法に強い、サポートベクターマシンという方法です。カテゴライズをする時に全体が少数で教師情報を全て与えることができるならば非常に高精度に分類してくれます。サポートベクターマシンについてはこちらが分かりやすいです。
- 教師なし学習
教師なし学習とは事前にサンプルデータが無い状態で実データ自体を解析する方法です。数値や言語の分類で使われます。レコメンドなどで推薦する商品の分類や、推薦対象となる顧客の分類をします。また自然言語の意味を解析することから商品の評判情報の解析などにも使えます。
1. k-平均法
k-平均法とは代表的なデータクラスタリング手法の一つで、計算を反復的に行いつつ、k個の集団に分類します。アルゴリズムが単純なため広く使われている手法です。
K-平均法は、一般には以下のような流れで実装される。
データの数を n 、クラスタの数を K としておく。1.各データ x_i(i=1... n) に対してランダムにクラスタを割り振る。
2.割り振ったデータをもとに各クラスタの中心 V_j(j=1... K) を計算する。計算は通常割り当てられたデータの各要素の算術平均が使用される。
3.各 x_i と各 V_j との距離を求め、x_i を最も近い中心のクラスタに割り当て直す。
4.上記の処理で全ての x_i のクラスタの割り当てが変化しなかった場合、あるいは変化量が事前に設定した一定の閾値を下回った場合に、収束したと判断して処理を終了する。そうでない場合は新しく割り振られたクラスタから V_j を再計算して上記の処理を繰り返す。
2.潜在意味インデックス(LSI)
潜在意味インデックスは類似した文章や顧客、商品などを見つける手法です。ベクトル空間モデルという仕組みを使います。これは単語という軸をとり、それらの出現頻度などを行列で表し、空間の1点として文書を表現します。こうしてデータの意味を捉えつつ分類します。
3.トピックモデル手法(LDA)
潜在意味インデックス(LSI)の発展版でデータの値の持つ意味を推定し分類します。確率分布を使ってデータを分類することが特徴です。
- 半教師あり学習
半教師あり学習とは少数のサンプルデータを用いてまずは学習を行い、その後ある程度の実データを分類してそのうち精度の高いものをサンプルデータと捉え直して再度教師あり学習を行っていく。これを繰り返すことで沢山ありすぎて教師情報を全部与えることが困難な場合でも教師あり学習の効果を期待できます。全商品をカテゴライズする時に食品、飲料品、衣類、電化製品、デジタルコンテンツ、スポーツ・・・と沢山ありすぎて全商品の教師情報を与えるのが難しい時に使います。
1.ブートストラップ法
ブートストラップと呼ばれる統計の手法があります。これは標本のデータから重複を許したサンプリング(普通は標本数と同じだけ)を行い、新たな標本を作製する、といった作業を何度も繰り返す手法です。この標本からのサンプリングという作業をリサンプリングと呼びます。こうして作られた複数の標本から計算される統計量(例えば平均、分散)のばらつき方は、母集団からサンプリングを何度も繰り返した時のばらつき方に近いという性質があります。つまり、複雑で難解な確率密度関数や中心極限定理を使うことなく、平均値や分散といった統計量がどのようにばらつく可能性を秘めているのかをあぶりだすことが可能なわけです。
- 構造学習
構造学習とはデータのラベルを個々に推定せず、データをまとめて渡すことで個々のラベル推定を一緒に行うことです。例えば一語一語何の品詞か推定するのでなく、文章丸ごと渡してその文章内の品詞の推定結果を一覧にする。これにより個々のラベル推定をデータが持っている構造に最適化した形で行うことができる。商品解説文全部から何の品詞かを推定し、構造を見ながらラベリングしていくことでカテゴリーデータベースを作っていくという時に使います。
1.構造化SVM
構造化SVMは性質上、日本語入力処理やかな漢字変換などで多く研究がされています。
https://research.preferred.jp/wp-content/uploads/2011/01/nlp2011-tkng.pdf
2.CRF
構造化SVMにおいてあるラベルに分類されるかどうかの確率値も算出し、高度な推定を行います。
- 強化学習
強化学習は教師あり学習とは異なり、教師情報は存在しません。代わりに学習した後から報酬というフィードバック情報を得ることで、さらなる学習の手がかりとします。リアルタイムのデータは不確実性のある環境なので報酬はノイズや結果が出るタイミングにばらつきもあります。利用者の反応を取り込みつつシステムやサービスを最適化していく時などに使います。例えばレコメンドや商品検索で顧客の反応を取り入れて結果を随時改善していくのに強化学習が使われます。広告のパーソナライズでも良く使われています。
1.バンディットアルゴリズム
バンディッドアルゴリズムとは限られたリソースの中で報酬(利用者の好反応)がどれぐらい得られるか過去に経験した過去の手段の「活用」と今後さらに得られるかもしれない未知の手段の「探索」という2種類の行動を使い分けて報酬を最大化する手法です。
- ディープラーニング(深層学習)
近年目覚ましい進歩を見せている手法です。ディープラーニングが注目された一つの経緯として、2012年の画像認識コンテストILSVRC 2012
http:// http://www.image-net.org/challenges/LSVRC/2012/results.html
においてディープラーニング(SuperVisionと表記)によって、2位以下と圧倒的な差をつけて優勝したことがあります。人の脳の構造を模倣するニューラルネットワークという手法を多層化し、高度化を図ったものです。多層化していることにより教師あり、教師なしの両方の機能を組み合わせてデータを様々な抽象度で学習できます。特に画像認識や物体認識の分野で盛んですが、 ECでもレコメンドや商品情報の解析、欠損情報の推定など広範囲に高度に活用ができ始めています。
1.制限付きボルツマンマシン
RBM(Restricted Boltzmann Machine)とは、Deep Learningにおける 事前学習(Pre Training)法の一種で、良く名前を聞く AutoEncoderと双璧を為すモデルの1種です。統計力学に端を欲し、1984年~1986年にモデルが考案されました。入力を受けて出力が 決定論的(deterministic) に決まるAutoencoderとは違い、議論を確率分布の上で行える 生成モデル であるため、利便性の高いモデルとして知られています。
今回の記事を書くにあたり、下記書籍による楽天技術研究所代表の森氏の寄稿を参考にしました。

更に良いサイトあるよというご指摘があれば教えてください
何かのご参考になれば幸いです。それでは
数学の大統一に挑む②ーガロア群、リー群、そしてラングランズ・プログラムとは何か
皆さんこんにちは。
前回書いた「数学の大統一に挑む①-群論からフェルマーの最終定理まで」はおかげさまで多くの方にご観覧頂きありがとうございます。
今回は後編です。
前回の知識がかなり必要となってきますので①を読んでない方は前からお読みいただけると幸いです。↓
主に数論的見地からラングランズプログラムとは何かというポイントだけまとめておりますのでリーマン面など幾何学的見地は豪快に飛ばしております。もっと知りたい!というお方は是非本をご購入ください。

第7章 ガロア群。数の対称変換について
さて、私たちはある年に生まれ、電話番号を持ち、たいてい口座番号を持っています。これらの数は1という数に1自身を幾つか加えることで作られています。こうしてできた数を自然数といいます。他に0という数や負数もあります。これらをまとめて整数といいます。さらには分数も含めた有理数があります。しかし数の中には有理数ではないものもあります。たとえば2の平方根。この有理数にはない新しい数の体系にはある秘密の特徴が隠されているのです。この数の体系はいくつかの「対称変換」を持っているのです。他の言い方をすれば、同じ体系に属する別の数に変換するルールを持っていると言えます。
 は方程式
は方程式の解であります。
 *
* =2と確かに成立します。しかし実を言えばこの方程式には解が2つあるのです。ひとつは
=2と確かに成立します。しかし実を言えばこの方程式には解が2つあるのです。ひとつは 、もうひとつは
、もうひとつは です。例えばx+y
です。例えばx+y を入れ替えてx-y
を入れ替えてx-y 、これを元に戻すとx-(-y
、これを元に戻すとx-(-y )=x+y
)=x+y 、と全く元に戻る恒等変換が起こります。このように
、と全く元に戻る恒等変換が起こります。このようにといった同じルールを持つある数に対して別の数に変換する事を対称変換と言います。
そして加法や乗法の操作を保存するような数体の恒等変換・対称変換の群をガロア群と言います。
もう一つ例をご紹介します。
前回はフェルマーの最終定理について見ていただきましたがフェルマーの小定理というものもあるということをご存知でしょうか?時計を見るとき我々は8時の6時間後を考えるときに8+6=14であるのに午後2時と考えます。この考え方が「12を法とする」といいました。pを法とする算術において「任意の数をp乗するとはじめと同じ数に戻る」のです。
たとえば3を法とする算術でa=2の時、2*2*2=8だけど3を法としているので
もう一つ、5を法とする算術でa=4の時、4*4*4*4*4=1024だけど5を法としているので
小定理と言ってもコンピュータのRSA暗号の基礎理論となるくらい極めて強力な定理です。このことは、数をp次のべきにするという操作、つまりaをにする乗法の操作を保存する恒等変換操作は、p個の元からなる有限体のガロア群だということを意味します。
第10章リー群
群とは下記性質を満たす集合でした。
任意の二つの元に集合の元を一つ操作させます。例えば整数の集合は、加法という操作を持つ群です。
リー群の概念は元の集まりで図形が現れる群のことを言います。リー群はノルウェーの数学者ソフス・リーに由来します。空間の回転は明らかに群になります。2週以上の回転の結果は必ず一つの回転で実現することができるので結合法則となります。逆回転はマイナス元であり,無回転が単位元であると言えます。これを回転群と呼びます。3次元の回転をあらわす行列は球面になります。3行3列、行列式が1の直交行列という特殊な球面の回転群は特殊直交群「SO(3)」と呼ばれます。

第15章ラングランズ・プログラム(結論)
先日書いた数学の大統一に挑む①のフェルマーの最終定理の項に出てきた志村ー谷山ーヴェイユ予想は”任意の三次方程式”について、素数を法とする解の個数はあるモジュラー形式の「係数」であると述べました。さらにその”三次方程式”と”モジュラー形式”の関係は1対1が成立するという”3次方程式”とモジュラー形式との不思議なつながりがありました。ラングランスはこの関係だけじゃなく、もっと一般的なつながりがあると考えました。そしてモジュラー形式の代わりとして、リー群Gの時は解析学などで使われる保型表現がそれであると気付きました。そして一番面白いところはラングランズは保型表現が別のリー群のガロア群と繋がっているということを見抜いたのです。この時の別のリー群LGを「リー群Gのラングランズ双対群」と呼びました。そこから研究を進め、どのリー群Gに対しても別のリー群LGが存在し、リー群LGのラングランズ双対群はもとのリー群Gとなることが分かりました。特に球面の特殊直交群SO(3)の場合は2重被覆、つまりSO(3)の各要素に対してラングランズの相対群の2つの要素が存在することが分かったのです。例えて言えば別の世界の体重、身長、年齢といった全ての特徴が同じ男と女が存在し、男は女になり、女は男になるのです。なぜそんなことが起こるのか今も分かっていません。2つの異なる三次元表現があるという数学的見地から物理学者は陽子や中性子よりも小さなクォークと反クォークを発見しました。さらには電気力と磁気力を入れ替えるマクスウェルの古典的な電磁気理論にもラングランス相対群LGが隠されていることが分かり始めています。現在、数論、調和解析、幾何学、表現論、数理物理学、量子物理学に至るまで実例を探し、なぜこんなことが起こるのか、それが何を意味するのかについてさらなる手がかりを探しているのです。
エドワード・フレンケル氏と訳者青木薫氏に感謝^^
数学の大統一に挑む①-群論からフェルマーの最終定理まで
皆さんこんにちは
この度青木薫さんの翻訳で新しい数学の本が出たので早速購入しました。

青木薫さんといえば世界最先端の数学の深遠な世界を、物語風に分かりやすく説明してくれる翻訳の第一人者です。
他にも
- 「無限」に魅入られた天才数学者たち (〈数理を愉しむ〉シリーズ) | アミール・D・ アクゼル, 青木 薫 | 本 | Amazon.co.jp
- Amazon.co.jp: フェルマーの最終定理 (新潮文庫): サイモン シン, 青木 薫: 本
- Amazon.co.jp: 暗号解読―ロゼッタストーンから量子暗号まで: サイモン シン, Simon Singh, 青木 薫: 本
などがありどれを取っても珠玉の出来ですので是非ご興味あればご一読ください。
今回のテーマは「ラングランズ・プログラム」ということです。
本の紹介を見ると
「ブレイド群」「リーマン面」「ガロア群」「カッツ・ムーディー代数」「層」「圏」…、まったく違ってみえる様々な数学の領域。しかし、そこには不思議なつながりがあった。やがて少年は数学者として、異なる数学の領域に架け橋をかける「ラングランズ・プログラム」に参加。それを量子物理学にまで拡張することに挑戦する。ソ連に生まれた数学者の自伝がそのまま、数学の壮大なプロジェクトを叙述する。
つまり数学の分野を横串にして扱える統一理論が現在数学界で起こっている最先端、このラングランズプログラムだということです。
しかし・・・
読んでみるとこれがなかなか難しい。上記フェルマーや暗号解読の比じゃないです。自伝半分なのでさらっと読み飛ばすこともできるけどラングランズプログラムの一端にも触れられませんでした。
そこで改めて数学的な内容を復習しつつそちらの面からまとめていくことにします。
第5章 群とは
群という概念はエヴァリスト・ガロアという神童が20歳の決闘前日に大急ぎで書きなぐった数学界の至宝です。
一般的な群の特徴はそんなに難しくありません。
この条件が満たされると群と呼びます。
結合則が成り立つということは,一連の演算があったときに『どこから手をつけてもいい』ということです.
がなりたつので,これに括弧をつけず,
のように書いてしまっても混乱はない,という主張でもあります.もしも結合則が成り立たないと,連続的に演算を行うのがえらく不便になります
群の公理に関しては群の公理 [物理のかぎしっぽ]が分かりやすいです。
因みにこれに
交換法則:a+b=b+a
が成り立つと「アーベル群」と呼びます。
ガロアは「演算の本質は,対象物(数など)そのものにあるのではなく,対象物の間に成り立つ算法の法則こそが大事なのだ。」と考えました。つまりそれまで古代バビロニア以降、数学とはいわばアルゴリズム(解法)の研究であったのに対し、扱う対象も,その対象に成り立つ演算も,すべて抽象化してしまって,『演算対象と,その間に成り立つ演算という構造だけ』を抜き出して考えるという,いわば代数学の抽象化が19世紀に進みました。
第7章 大統一理論。ロバートラングランズについて
数学には様々な領域がある。それらの領域はしばしば別の大陸のように感じられる。・・しかし彼の野望は単に少数の島をつなぐというだけに留まらなかった。1960年代の末に彼が創始したラングランズ・プログラムは今日ではたくさんの島に橋をかけるメカニズムを見出そうという運動に発展している。ラングランズは現在、プリンストンの高等研究所で数学の名誉教授となっている。それは、かつてアルベルト・アインシュタインが在籍していたところである。
第8章 フェルマーの最終定理ー背理法による証明ー
の解となるn=3 以上のx,y,zは存在しないというものです。
余談だけど本書P143にはnが2以上と書かれているけどn=2はなどで存在するので誤植です。
1994年10月にアンドリュー・ワイルズによって証明を発表。1995年のAnnals of Mathematics誌において出版し、その証明は、1995年2月13日に誤りがないことが確認され、360年に渡る歴史に決着を付けました。
こちらがその論文です。
http://math.stanford.edu/~lekheng/flt/wiles.pdf
それでは解決に至るまでの一連の経緯を記述します。
「Nを法とする」
時計を見るときにこの算術を使います。我々は8時の6時間後を考えるときに8+6=14であるのに午後2時と考えます。この考え方が「12を法とする」といいます。
例えば
という3次方程式において「5を法とする」と考えるとx、yにそれぞれ何がはいるでしょうか?
簡単なところではx=0,y=0があります。x=1,y=4でも16+4=1−1となり20=0ですが、ここで5を法としているので0=0が成立します。他にもx=0,y=4。x=1,y=0の「4通り」の解が存在します。
よく
「1+1は2にならない世界もあるんだぜ」
という人がいますがこれは2を法とした場合1+1=0となるからです。
閑話休題。ここでpを法とする解の個数を探すことにします。p=5のときは当然p=7やp=11といったときとは解の数が異なるのはイメージつくと思います。この方程式のpを法とする解の個数はpにどのように依存しているのだろうか。数学者たちはしばらく前からおよそpと解の個数が等しいことを知っていました。実際の解の個数との差を「不足」と呼びで表すことにします。つまりpを法とする解の個数は
で表されます。
pとpを法とする解の個数は一見ランダムに見えます。しかし全てのを一挙に生成する、シンプルな規則があるとしたらどうでししょうか。1954年ドイツの数学者マルティン・アイヒラーがまさにそんな規則を見出したのです。
括弧を外すと次のような無限級数を得ます。
この係数1,-2,-1,2,1,2,-2...がそれぞれの乗数を法とする”先ほどの三次方程式”のpを法とした場合のpと実際の解の個数との差「不足」
を表しているのです。
先ほどp=5を法とする3次方程式の場合について、解が4つあると言いました。5乗のところを見ると係数は1。つまり5-1で解は4個と確かに正しいことがわかります。
つまりこの一行の式が、”先ほどの三次方程式”の解の個数に関する全ての情報を含む、秘密のコードなのです。この方程式の解は生物ではDNA分子にコードされていることが知られています。・・アイヒラーの驚くべき洞察は、素数を法とする”三次方程式”の解の個数は、ランダムに分布しているように見えるが、実は調和と秩序がとれているということを見抜いたことです。・・志村ー谷山ーヴェイユ予想は、アイヒラーの得た結果を一般化しました。この予想は”任意の三次方程式”について、素数を法とする解の個数はあるモジュラー形式の「係数」であると述べました。さらにその”三次方程式”と”モジュラー形式”の関係は1対1が成立するという驚くべき予想でした。ここでフェルマー方程式である種の”三次方程式”が作り出すことができると仮定します。しかし、ケン・リベットがその”三次方程式”の素数を法とする解の個数は、志村ー谷山ーヴェイユ予想によって存在が約束されているモジュラー形式の係数ではあり得ないことを示しました。つまり志村ー谷山ーヴェイユ予想が証明されればそのような”三次方程式”は存在せず、フェルマーの方程式にも解は存在しないということが証明されるとなるわけです。これをワイルズは証明したのです。
意識と人工知能ロボット
最強の地図API「Google Maps JavaScript API v3」を使って外国人用のレストランガイド作りました
皆さんこんにちは。
今週末時間があったので今日は地球上でもっとも使いやすい地図APIであるGoogle Maps JavaScript API v3 を使ってどこまで出来るか調べてみるついでにレストラン情報サイトを作ってみました。
コンセプトは全く右も左も分からない外国人がサイトを見て食べたい種類のレストランに何とかたどり着けるようにすることです。
スクリーンショットはこちら。
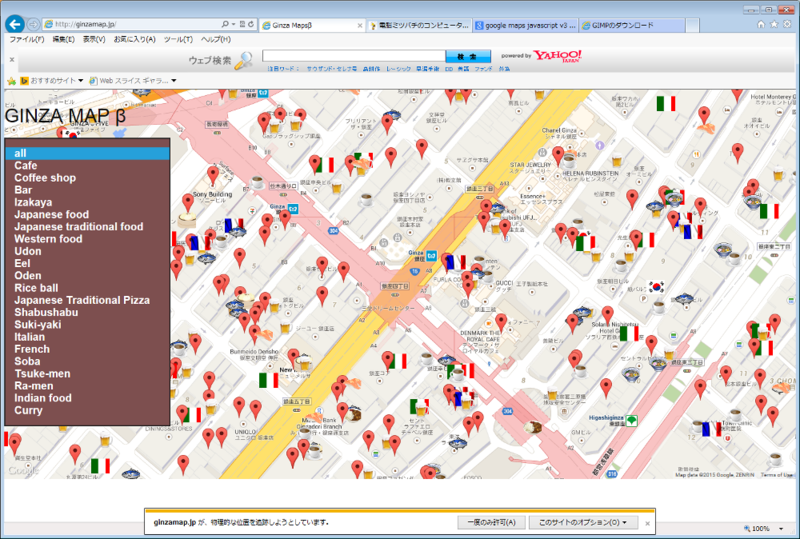
カテゴリごとにアイコンをつけ、銀座周辺にいたらその場所が表示され(今のところあんまり正確じゃないです)いなければ和光から始まります。
タブによってイタリアンやラーメン屋などを絞って検索することが出来ます。
まず最初に緯度経度、カテゴリーが分かるレストラン情報をぐるなびさんかロケタッチさんからいただきます。
今回はロケタッチさんから頂きました。
http://api.gourmet.livedoor.com/v1.0/restaurant/?api_key=API_KEY&area_id=1&page=??
のような形で適当にphpとかでページ番号をエラー吐くまで繰り返して足していき、データベースにレストラン情報を入れていきます。
私の今回のDB設計は
+---------------+--------------+------+-----+---------+----------------+
| Field | Type | Null | Key | Default | Extra |
+---------------+--------------+------+-----+---------+----------------+
| id | int(11) | NO | PRI | NULL | auto_increment |
| name | varchar(128) | NO | | NULL | |
| address_j | varchar(255) | YES | | NULL | |
| address_e | varchar(255) | YES | | NULL | |
| address_c | varchar(255) | YES | | NULL | |
| address_t | varchar(255) | YES | | NULL | |
| zip | varchar(11) | YES | | NULL | |
| category1 | varchar(255) | YES | | NULL | |
| category2 | varchar(255) | YES | | NULL | |
| category3 | varchar(255) | YES | | NULL | |
| tel | varchar(30) | YES | | NULL | |
| url | varchar(255) | YES | | NULL | |
| url2 | varchar(255) | YES | | NULL | |
| closeday | varchar(255) | YES | | NULL | |
| closeday_note | varchar(255) | YES | | NULL | |
| weekday | varchar(255) | YES | | NULL | |
| lunch | varchar(255) | YES | | NULL | |
| dinner | varchar(255) | YES | | NULL | |
| name_e | varchar(255) | YES | | NULL | |
| lat | varchar(20) | YES | | NULL | |
| lng | varchar(20) | YES | | NULL | |
| rate | varchar(20) | YES | | NULL | |
+---------------+--------------+------+-----+---------+----------------+
こんな感じにしました。思いつくままに作ったので非常に雑なDBです。使わなかったやつとかいっぱいあります。^^;
大事なのは 名前、住所、緯度、経度、カテゴリ情報、開店時間、休業日、ランチの値段、ディナーの値段、電話番号くらいでしょうか?
大体2400件くらいの銀座周辺のレストラン情報を頂いたのでいよいよgooglemap APIを使ってみます。
重要なのはいかにして質のよいサンプルコードに行き当たるかです。幸いにしてGoogleが質のよいコードを公開しているので使わせてもらいます。
Code Samples - Google Maps JavaScript API v3 — Google Developers
上記サイトにやりたいこととサンプルコードが入っていますので一番上のsimple mapをクリックしてコードを見て見ます。
index.html
<!DOCTYPE html>
<html>
<head>
<title>Simple Map</title>
<meta name="viewport" content="initial-scale=1.0, user-scalable=no">
<meta charset="utf-8">
<style>
html, body, #map-canvas {
height: 100%;
margin: 0px;
padding: 0px
}
</style>
<script src="https://maps.googleapis.com/maps/api/js?v=3.exp"></script>
<script>
var map;
function initialize() {
var mapOptions = {
zoom: 8,
center: new google.maps.LatLng(-34.397, 150.644)
};
map = new google.maps.Map(document.getElementById('map-canvas'),
mapOptions);
}
google.maps.event.addDomListener(window, 'load', initialize);
</script>
</head>
<body>
<div id="map-canvas"></div>
</body>
</html>
実にこれだけでマップが表示できることになりました。
これを元手にデータベースの緯度経度情報からマーカーに落とし込んで見ます。
マーカーのへの情報はこの方が分かりやすいサンプルコードを書いてくれております。
マーカーの作成 - マーカー - Google Maps API入門
var m_latlng1 = new google.maps.LatLng(35.632605,139.88132);
var marker1 = new google.maps.Marker({
position: m_latlng1,
map: map
});
こんな感じで緯度経度を指定します。今回のマーカーは2000を越えるため配列にして処理します。
次にそんなに正確には測れないのですがgeoLocationというhtml5の新機能で非常に簡単にGPSみたいなことが出来るのでを使ってみます。
銀座周辺にいれば該当する場所からの表示を行います。
//geolocationinit
// Try HTML5 geolocation
if(navigator.geolocation) {
navigator.geolocation.getCurrentPosition(function(position) {
//銀座以外はデフォルト
if(position.coords.latitude>35.672135&&position.coords.latitude<35.674617){
if(position.coords.longitude>139.757802&&position.coords.longitude<139.777705){
var pos = new google.maps.LatLng(position.coords.latitude,
position.coords.longitude);var infowindow = new google.maps.InfoWindow({
map: map,
position: pos,
});map.setCenter(pos);
}
}
}, function() {
handleNoGeolocation(true);
});
}
コードは実にこれだけ。
銀座以外はデフォルトの和光からにしたいので銀座の緯度35.672135~35.674617、経度139.757802~139.777705を判定してもらいます。
さて、続いてresponse.phpとかを作成し、mysqlの情報をphpで取り出したあとは、下記コードでjsonにエンコードし、javascriptに投げてあげます。
response.php
header('Content-type: application/json');
echo json_encode($spot);
受ける側のindex.htmlではjQueryのajaxを使って非同期で読み込みを行います。
jQueryとjquery.jsonというプラグインを使用します。
jquery.json-2.4.js - jquery-json - Full source of the plugin - jQuery JSON - Google Project Hosting
php側ではjson以外の情報を一切出さないようにしないとajaxが受け取るときにはてな?っとなってしまいます。
この方のJSONの処理が参考になりました。ありがとうございます^^
jQuery & Ajax通信を使ってPHPにPOSTでデータを送信するサンプル – WebCake
ここで成功したらデータのカテゴリによってアイコンを変える処理をします。
面倒くさいのでべた打ちします。
//iconsetting
var Icon_beer = new google.maps.MarkerImage("icon/beer.png");
Icon_beer.size = new google.maps.Size(35, 35);
Icon_beer.anchor = new google.maps.Point(0, 35);
var Icon_china = new google.maps.MarkerImage("icon/china.png");
Icon_china.size = new google.maps.Size(35, 35);
Icon_china.anchor = new google.maps.Point(0, 35);
var Icon_coffee = new google.maps.MarkerImage("icon/coffee.png");
Icon_coffee.size = new google.maps.Size(35, 35);
Icon_coffee.anchor = new google.maps.Point(0, 35);・
・
・
/**
* Ajax通信が成功した場合に呼び出されるメソッド
*/
success: function(data,dataType)
{
//結果が0件の場合
if(data == null) alert('データが0件でした');
dataglobal=data.length;
//返ってきたデータの表示
content = $('#content');
var markers = new Array();for (var i =0; i<data.length; i++)
{
var m_latlng = new google.maps.LatLng(data[i].lat,data[i].lng);
if(data[i].category1=="バー" || data[i].category1=="ビアホール
・ビアガーデン" ||data[i].category1=="居酒屋"||data[i].category1=="和食その他"){
markers[i] = new google.maps.Marker({
position: m_latlng,
icon: Icon_beer,
map: map
});
}else if(data[i].category1=="北京料理" || data[i].category1=="台湾料理" ||data[i].category1=="中華料理その他"){
markers[i] = new google.maps.Marker({
position: m_latlng,
icon: Icon_china,
map: map
});以下同文
最後にプルダウンメニューから変更があった場合、カテゴリを読み直してphpに渡してあげます。
ここの処理も上記参考サイトを見ていただくとよいかと思います。
jQuery & Ajax通信を使ってPHPにPOSTでデータを送信するサンプル – WebCake
これで大体の処理が終わりましたので後はデザインをちょっと整えて完成です。
今回は大きく分けて
- apiを使ったデータベースへの入力処理 (php)
- データベースを使ったサーバサイドプログラム。jsonで出力処理 (php)
- サイトに表示するjavascriptを含んだhtml (html+javascript)
の3つのファイルを作りました。
実際動かして外国の皆様に信頼に足る情報を使ってもらえるには食べログさんの情報がほしいですね。
また暇を見て改良してみます。
ではまた。 ^^
追記:夜調べたらぐるなびさんが英語版の店情報を出しており実装したらぐるなびに加入出来るトラディショナルなお店が残りかなり良い感じになりました。止まらなくてつい徹夜仕事になってしまったorz
追記2:2015年11月iPhoneアプリにしました。
ポータブルなハッカー御用達デバイス作った
皆さんこんにちは。









vi /etc/network/interfaces
auto lo
iface lo inet loopback
allow-hotplug wlan0
iface wlan0 inet dhcp
wpa-driver wext
wpa-ap-scan 1
wpa-scan-ssid 1
wpa-key-mgmt WPA-PSK
wpa-proto WPA2
wpa-pariwise CCMP
wpa-group CCMP
wpa-ssid "接続先のSSID"
wpa-psk "接続先のキー"

未使用領域をoptにマウントします
fdisk -l
をおすと最初にデバイス名が出てきます。

私の場合/dev/mmcblk0なのでこの未使用領域にパーティションを割り当てフォーマットし、/optにマウントします。
参考になるサイト
fdisk /dev/mmcblk0
command: n #partition作成
select(default p) :p #primaryパーティション
Partition number :3 #partition ナンバー
First sector : #enterでデフォルトセクタから開始
Last sector : #enterで最大セクタまでの領域確保
command : w #書き込み
これで未使用領域のパーティションを確保できました。
ここからフォーマットし/optにマウントします。
フォーマット例
mkfs -t ext4 /dev/mmcblk0p3

mount /dev/mmcblk0p3 /opt
df -h #dfで確認してoptにデバイスが割り当てられていたら成功

起動時に/optのマウントやシェルを実行するため、/etc/profile.d/に適当な名前mountopt.shなどを作りコマンド「vi mountopt.sh」などで下記記入する
mount /dev/mmcblk0p3 /opt

